In the last issue of SBJ, Dave Gerr described how to make simple navigation devices for measuring speed, distance, and time.

In small craft navigation, it is both impossible and unnecessary to be extremely accurate. Instead, what you need is to get a quick mental image of where you are and where you're going. On short courses in a small boat, just eyeballing your heading or rolling a round pencil from your course line to the compass rose will sometimes be accurate enough.

In a small boat and a stiff breeze, your bearing angles are always going to be off by a degree or two or more because the motion of the boat, and your closeness to the water, means your instruments are subject to all sorts of minor errors that add up quickly. Stopping to get very accurate
bearings would only introduce additional error. So don't worry about the decimal points. Get the big picture in nice round numbers and you'll really know where you are all the time. When you know there are dangers near, you just set a course well clear of them.

Sailboats have an additional problem: They have to tack to weather. So, going to windward you still have to determine your course on each tack and how long to stay there. What's more, if the course you're sailing is not dead to windward, you'll have to stay on one tack longer than another. Naturally, there's a simple way to calculate all this, and it only takes a small piece of oaktag (heavy, smooth-surface, white cardboard).

(click to enlarge)

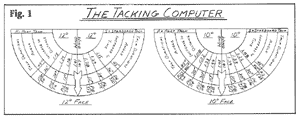
Cut the oaktag into a half-circle like a protractor and mark it with different angles at convenient intervals. On both sides, perpendicular to the straight edge, draw an arrow down the centerline from the straight edge to the curved edge. This arrow represents the wind direction. On either side of the centerline arrow, draw lines for angles every 10 degrees on one face and every 12 degrees on the other. At each of the angle lines, mark the proportion of time to spend on each tack, the relative wind angle, and the multiplier for the extra dislance to be covered. (Obviously, with the wind dead ahead, you spend the same amount of time on each tack.) You now have a tacking computer (Fig. 1). Cover it with clear contact paper and wax as you did the distance rule (See Part I).

To use your computer, mark out the baseline of your desired course on the chart and place the tacking computer on the chart so that the centerline of the straight edge lies anywhere along the length of the baseline. Then rotate the computer so that the wind arrow is at an angle across your course that matches the true wind angle. Flip the tacking computer over to use either the 10-degree or the 12-degree face). Now, simply read the time to spend on each tack from the angle line that falls on your baseline.

For example, if the wind is blowing across your course from port at about a 20-degree angle (true), then you would read "P17, S8 - 1.33" (Fig. 2). This means stay on the port tack for 17 minutes and on the starboard tack for 8 minutes. Also it tells you that the additional distance to be
covered is 1.33 times or about 33 percent more than the straight line or baseline distance.

The nice thing about all this is that it is so fast. It takes less than a minute to lay off a desired course and then to figure the extra time and distance. It is virtually unnecessary to put pen to paper. If your baseline course was 8 miles straight, then it would be 35 percent more in actual distance sailed (1.35 times or 35 percent more is close enough to 1.33 for our purposes). In this case, your actual distance sailed is about 10.8 miles. If you were traveling at 5 knots, your estimated time of arrival would be 2 hours and 10 minutes (10.8 miles ÷ 5 knots = 2.16 hours). It's handy to remember that 0.16 hour = 10 minutes (approximately) and that 0.1 or 1/10 hour = 6 minutes. All of this figuring can be done rapidly on Gerr's Nomograph (See Part I).

Short Tacks & Long Tacks
Another useful thing to remember is that at about half your time on each tack you will cross your baseline. This is important because) if the wind is fluky, you will want to be sure to make short tacks. This will reduce the chance of being pushed further downwind by headers and allow you to take advantage of good lift. Also, if you have to go through a narrow channel at some point on your course, you can wait until you are crossing your baseline course and then make very short tacks close to the baseline, until you are clear.

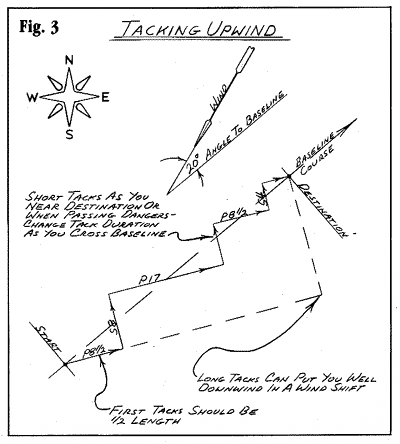
To make short tacks you need only halve or quarter the times shown on the tacking computer. On the other hand, if
you are on a particularly long course, you can double or triple the times. None of this affects the relative amounts of time required on each tack or the additional distance covered; you can change from short to long tacks as often as you like, as long as you spend the same proportion of time on each tack and you change tacking durations when you cross your baseline (Fig. 3).

The tacking computer assumes that your boat makes good a course about 45 degrees to the true wind, or that you tack in 90 degrees. This is the case for almost every vessel I've been on, although some do better and some do worse. When it is blowing hard, especially when it has been blowing hard for a while, I add to the distance factors. This is to make up for the increasing leeway you (and the water) will be making. For winds from 18 to 25 mph, I add from 5 to 10 percent, and for winds from 25 to 30 mph, about 15 to 20 percent If it's blowing much harder than this and you have to get to windward, good luck! Even at 30 mph, most small boats are making very little progress to
weather.